Special Challenges — Roots

When root functions are involved in the denominator, finding the essential degree of the denominator is more difficult. Even when the root functions are in the numerator, extra care must be taking when dividing each term in the numerator and denominator by the essential degree degree of the denominator.

If x > 0, then note that x = √---
x2 . When x →∞ we know that x > 0 and so

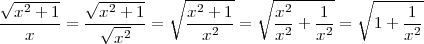
√ -2---- √ -2---- ∘ --2---- ∘ --2----- ∘ ------- --x--+-1= --x√-+-1-= x-+-1-= x-+ 1--= 1+ 1-- x x2 x2 x2 x2 x2

[Recall that √-2--
-xx+1-

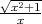and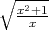

are not equal!!!]

If x < 0, then note that x = - ---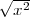
√ x2 . When x →-∞ we know that x < 0 and so

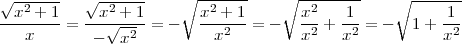
√ ------ √ ------ ∘ ------- ∘ -------- ∘ ------- --x2 +-1 --x2-+-1 x2 +-1 x2- 1-- -1- x = - √x2-- = - x2 = - x2 + x2 = - 1 + x2

Return to the Limits at Infinity page.