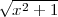 is
is 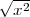 , which is x
(for positive x) or -x (for negative x).
, which is x
(for positive x) or -x (for negative x).
Essential Degree
The essential degree (their normal degree) is fairly straightforward to determine for a polynomial, but for root
functions this takes a little more effort. For instance, the essential degree of 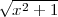 is
is 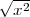 , which is x
(for positive x) or -x (for negative x).
, which is x
(for positive x) or -x (for negative x).
To determine the essential degree of 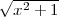 above, we dropped all terms under the radical sign except
that term whose exponent gave us the degree of the polynomial underneath the radical sign. We isolate
this highest powered term because as x gets bigger while x →∞ , the term with the highest power of x
dominates the others:
above, we dropped all terms under the radical sign except
that term whose exponent gave us the degree of the polynomial underneath the radical sign. We isolate
this highest powered term because as x gets bigger while x →∞ , the term with the highest power of x
dominates the others:
| x = | 10 | 1,000 | 1,000,000 |
| x2 = | 100 | 1,000,000 | 1,000,000,000,000 |
| x3 = | 1000 | 1,000,000,000 | 1,000,000,000,000,000,000 |
or as x →-∞:
| x = | -10 | -1,000 | -1,000,000 |
| x2 = | 100 | 1,000,000 | 1,000,000,000,000 |
| x3 = | -1000 | -1,000,000,000 | -1,000,000,000,000,000,000 |
so we see that when x gets larger and larger, the contributions by the terms with the smaller exponents will be negligible.
Similarly, the essential degree of 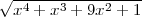 is
is 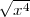 is x2.
is x2.
Return to the computation page.
Return to the Special Challenges page.
Return to the Limits at Infinity page.