Temperature Measurements

Temperature measurements in todays's engineering environment encompasses a wide variety of applications. Over the last decades, engineers have developed a wide array of temperature sensors and devices to handle this demand. Temperature is a very critical and widely measured variable for most engineering fields. Many processes must have either a monitored or controlled temperature requirement. This can range from the simple monitoring of the water temperature of an engine or load device, or as complex as the temperature of a weld in a laser welding application. A simple and elegant solution to measure temperature was developed by Thomas Johann Seebeck in as early as 1821. He discovered that a circuit made from two dissimilar metals with a junction would deflect the needle of a compass (the multimeter of the day). He soon realized that the metallic dissimilarity caused an electrical current to flow through the wires, as seen in the following schematic

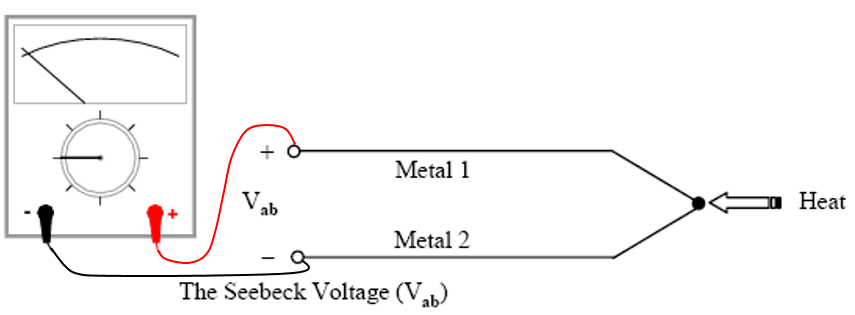
Paragraph

Experimental Setup

Paragraph

Arduino Hardware Code

Paragraph

Acquire and Plot Temperature with Python

The following Python script PARAGRAPH To run this script, please copy it and paste it in your python editor.

			
#-------------------- Rational of the data analysis code ---------------------------
# This code does the follwing:
#     1) extracts the distance values from the csv data file (that we measured
#        previously)
#     2) sorts these values for each position where we measured
#         *  I measured mine in a range of 1 to 20-inch in increments of 1-inch
#     3) Calculates the mean value and the stardand deviation from the sorted
#        values of each location
#     4) Plots the mean values with error bars at 95% Confidence Intervals
#     5) Compares these mean values with the true values that we expected to have,
#        i.e. 1, 2, 3, ... 20-inch

# --------------- Import modules that we need --------------------------------------
import numpy as np
import matplotlib.pyplot as plt



# Some additional commands (at your choice) to set font globally
# as times new roman, italic, and bold for nicer plots
plt.rcParams["font.family"] = "Times New Roman" 
plt.rcParams["font.style"] = 'italic'
plt.rcParams["font.weight"] = 'bold'
plt.rcParams["font.size"] = 14

# -------------------- Import the csv data file that was saved --------------------
dat = np.loadtxt('Distance_Measurement_Wood_block.csv', delimiter=',', skiprows = 1)
Time = dat[:,0] # The first column was time in seconds
Dist = dat[:,1] # The second column was the distance


Means = []# Create an empty array of to collect the mean values as they are extracted
Stds = [] # Create an empty array of the standard deviation values

# --------- Separate Distance Data in Bins of 1, 2, 3, ... 20-inch (in my case) -----
# Use a for loop to collect all the distance values that fall within a range of
# -0.5 inch to +0.5 inch of the intended distance.
#       For example, all the measured distance values between 0.5 to 1.5-inch will be
#       collected in the bin for 1-inch distance

for i in range(1,21):
    # the 'where' numpy function helps to get the indexes of the values
    Indexes = np.where(np.logical_and(Dist >= i-0.5, Dist <= i+0.5))
    Sorted = Dist[Indexes]# Drop the distance values within each bin
    Mean = np.mean(Sorted)# Calculate the mean value of the bin
    Std = np.std(Sorted)  # Calculate the standard deviation value of the bin
    Means.append(Mean)    # Append the calculated mean value in the array 
    Stds.append(Std)      # Append the calculated std in the array

# ---- In case that we want to see how the analysis works until this point
print("mean = ",Means)
print('Std = ',Stds)

# Generate an array of equally spaced values from 1 to 20 as our true values
TrueValues = np.linspace(1,20,20)

# Calculate the Confidence Intervals as two standard deviation above and two standard
# deviation below the mean value. This is required to get a probability of 95% 
CI = np.multiply(Stds,2)

Mean_CI = np.nanmean(CI) # Calculate the mean value, any nan, "not a number", is removed
print('Mean CI: ',Mean_CI)

# ------------- Plot the Measured Distance and Its Confidence Intervals ------------
fig = plt.figure(1)
plt.clf()
plt.errorbar(TrueValues,Means,yerr=CI,fmt ='bo', markerfacecolor='none',
             capsize=2,ecolor='red', label='Measured')

plt.plot(TrueValues,TrueValues,'--b.', label='Expected Value')
plt.xlabel('Distance, true value, [in]')
    
plt.ylabel('Measured distance, [in]')
##plt.axis([0, 5, -3, 4])
plt.grid(True)
plt.grid(linestyle='dotted')
ax = plt.gca()
ax.set_position([0.15,0.17, 0.75, 0.75])# adjust margins of the figure
plt.legend()# show legend on the graph


plt.show()# needed when we use IDLE

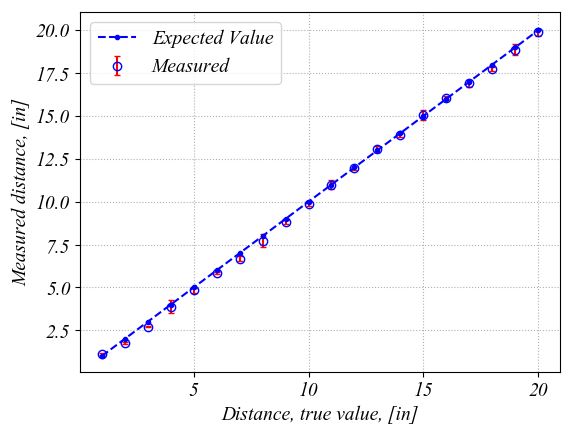
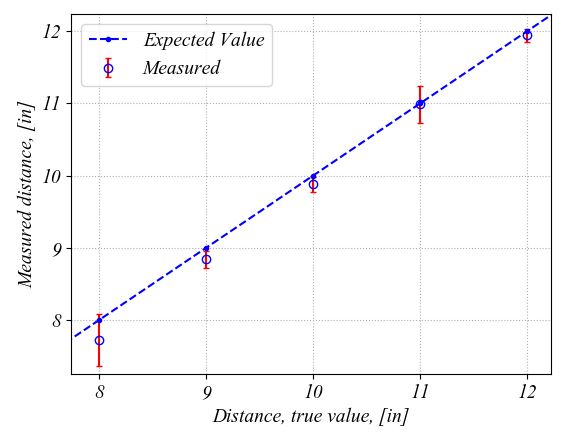
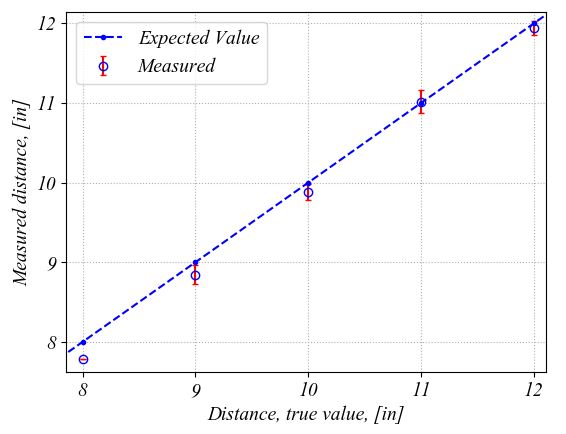
Python plots the following figure. The plot on the right is a zoom in to better show the errorbars and the markers. The errorbars represent the 95% confidence intervals with two stardard deviations above and below the mean value for each location. As we talked above, the true value on the graph represents an estimated value. It is here just for a comparison with the distance measured with the ultrasonic transducer. These plots show that overall, the ultrasonic transducer performs well. In some locations, the errorbars are larger and this might be caused by the fact that I might have move the wood block slower and I captured points while I was moving it.

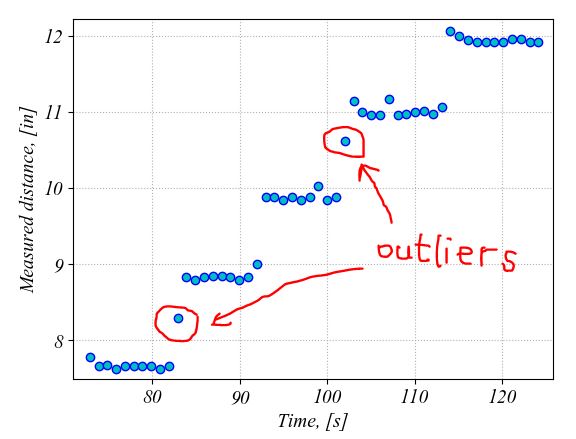
If we change the indexes search range in the for loop, i.e. the "Indexes" line in the for loop, from ± 0.5 from the expected value to ± 0.25, then the precision is increased. This means that the 95% confidence intervals are much tighter this time as it can be seen in the following zoom in the figure. By using a tighter range for selection of the measured distance values at each location, we remove the outliers that were introduced from moving the wood block too slow in the desired position. For example, such outliers were removed from locations at 8-inch and 11-inch distance from the transducer by using a tighter selection interval when calculating the mean and standard deviation values.

Thus the smaller the confidence intervals are the higher the precision of the measurement will be. After we removed the outlier data points caused by recording data while moving the block into the position, the 95% confidence interval has an average value of ± 0.11-inch. We use the average value to characterize the confidence intervals since we want to minimize the effect of other features of our measurement setup. The average value is an indication of the precision of the whole measurement setup, not only of the ultrasonic transducer. As we have seen in the previous assignment, a tilt of the block might introduce errors in our measurements. Moreover, any loose jumper wire can also affect the precision. Thus, the final conclusion is that with our current setup, 95 points out of 100 fall within ± 0.11-inch of the mean value that represents the measured distance.