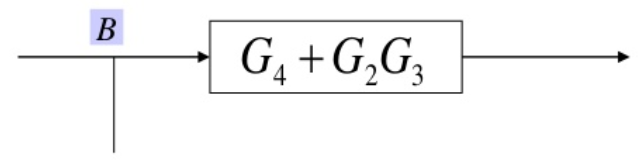Reducing Block Diagrams by using Octave/MATLAB

      Scientific programming languages, such as Octave, Scilab, Python, and MATLAB can simplify the burden of arithmetic operations so that the engineer can focus on the procedure of reducing the block diagrams (BD) rather than spending energy and time with simple, but tedious math of fractions. In this following example we will consider that we don't know the exact transfer function (TF) of each block. All we know are the symbolic names of the TF.

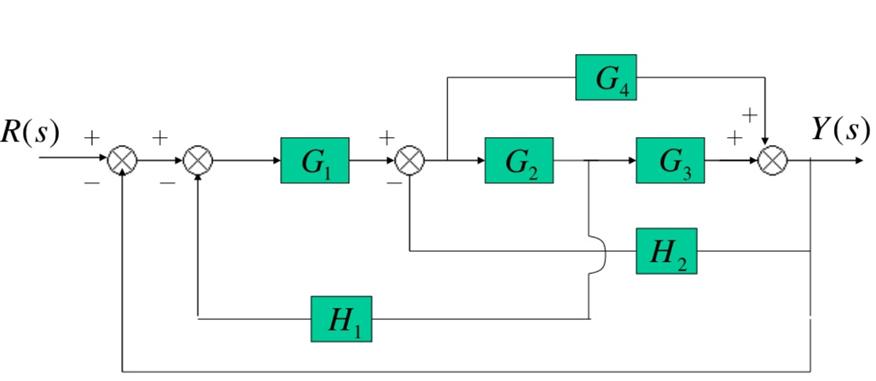
Example: Reduce the system shown below to a single transfer function T(s) = Y(s)/R(s).

Solution:

Moving pickoff point A ahead of block G₂ would help to reduce G₂ in series with G₃ and then both of them in parallel with G₄. To move the pickoff point we need to add another block G₂ as showed in series with H₁ - which is the block that uses the pickoff point B. This step can be configured as

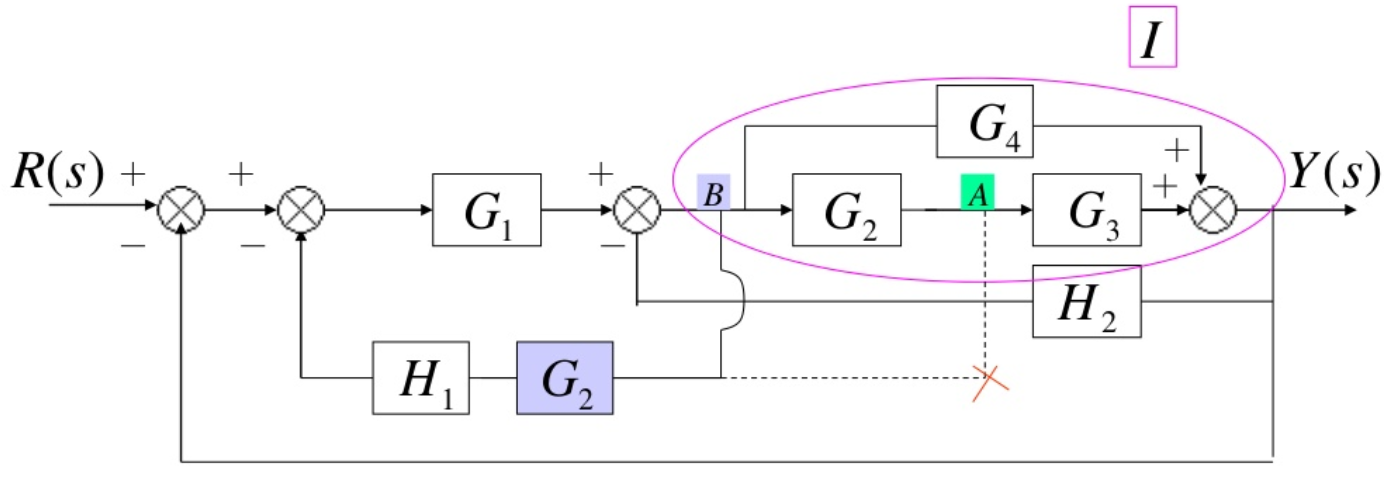
Thus, all the blocks inside the loop I can be simplified to